당신은 주제를 찾고 있습니까 “상관 분석 회귀 분석 – 상관분석 개념 설명- 깜신의 통계 왕초보 탈출 26탄“? 다음 카테고리의 웹사이트 https://you.charoenmotorcycles.com 에서 귀하의 모든 질문에 답변해 드립니다: https://you.charoenmotorcycles.com/blog. 바로 아래에서 답을 찾을 수 있습니다. 작성자 김종엽 이(가) 작성한 기사에는 조회수 21,962회 및 좋아요 248개 개의 좋아요가 있습니다.
상관 분석 회귀 분석 주제에 대한 동영상 보기
여기에서 이 주제에 대한 비디오를 시청하십시오. 주의 깊게 살펴보고 읽고 있는 내용에 대한 피드백을 제공하세요!
d여기에서 상관분석 개념 설명- 깜신의 통계 왕초보 탈출 26탄 – 상관 분석 회귀 분석 주제에 대한 세부정보를 참조하세요
상관분석은 두 개의 요인이 서로 어떤 상관이 있는지 알아보는 분석 방법이며, 회귀분석을 시작하기 위한 토대가 됩니다. 이번 시간에는 R스튜디오 실습에 앞서, 개념에 대해 살펴보도록 하겠습니다.
상관 분석 회귀 분석 주제에 대한 자세한 내용은 여기를 참조하세요.
[통계] 상관분석? 회귀분석? – 퐈니썬’s LIfe – 잘 실패하자 – Tistory
상관분석은 결국 두 변수에 대한 관계성을 파악하고, 어느 정도 그 관계성이 강한가를 보는 것이고, 회귀분석은 인과관계에 있는 두 변수가 어떤 변화 …
Source: panython.tistory.com
Date Published: 10/5/2022
View: 9370
제 11장 상관과 회귀분석
정도의 측도를 상관계수(coefficient of correlation)라 한다. 회귀분석에서 독립변수는 확정변수(조절되는 확률변수가 아닌 주어진 값)인 반면, 상관분석에서.
Source: contents.kocw.or.kr
Date Published: 8/24/2022
View: 1808
상관 관계와 회귀의 차이
상관 관계 는 ‘x’와 ‘y’의 두 변수 사이의 연관성 또는 연관성을 알 수있게 해주는 분석으로 설명됩니다. 반면에 회귀 분석은 독립 변수의 알려진 값을 기반으로 종속 변수 …
Source: ko.gadget-info.com
Date Published: 2/17/2021
View: 8698
3. 회귀와 상관
회귀와 상관. 3.1. 단순회귀분석(單純回歸分析, simple regression analysis). 원인과 결과의 관계가 있는 두 변수를 분석-> 회귀분석. 같은 개체에서 측정한 두개의 …
Source: jujc.yonam.ac.kr
Date Published: 9/10/2021
View: 7897
상관분석과 회귀분석 – KINX
피어슨 상관계수 r은 제곱하여 R²이라. 함. • 0< R² < 1사이의 값을 가지며 실제값, 예. 측값, 평균값을 비교하는 분산분석을. 통해서도 구할 수 있습니다.
Source: kocw-n.xcache.kinxcdn.com
Date Published: 4/21/2022
View: 3843
상관분석 및 회귀분석
④ 유의이면 x 에 대한 y 의 회귀선을 구함. ⑤ 결정계수(기여율, r2 )을 구함. 2.2 상관분석을 위한 산점도의 작성. 2.2.1 상관·회귀의 기초로서의 산점도.
Source: www.cpedua.com
Date Published: 12/10/2021
View: 3294
상관분석과 회귀분석 – 서울논문컨설팅
물론 그 모형은 모형적합도를 통하여 모형의 적합성을 확인될 것이다. 상관과 선형회귀분석의 차이는 그 목적성에 있다. 상관은 두 변수들간의 어떠한 관계 …
Source: www.seoulpaper.com
Date Published: 11/23/2022
View: 7074
주제와 관련된 이미지 상관 분석 회귀 분석
주제와 관련된 더 많은 사진을 참조하십시오 상관분석 개념 설명- 깜신의 통계 왕초보 탈출 26탄. 댓글에서 더 많은 관련 이미지를 보거나 필요한 경우 더 많은 관련 기사를 볼 수 있습니다.
주제에 대한 기사 평가 상관 분석 회귀 분석
- Author: 김종엽
- Views: 조회수 21,962회
- Likes: 좋아요 248개
- Date Published: 2017. 9. 27.
- Video Url link: https://www.youtube.com/watch?v=oM0thqtGbqI
[통계] 상관분석? 회귀분석?
728×90
2022.02.11 – [통계] – [통계] 독립 변수란? 종속 변수란?
독립변수와 종속변수에 대한 글에 이은 글입니다.
독립변수와 종속변수의 관계를 알아보기 위한 방법, 우리가 알고자 하는 현상에 대해 수학적으로 모델을 어떻게 풀어갈 것인가 에 대한 방법인 상관분석과 회귀분석에 대해 작성하고자 합니다.
<상관분석>
제가 생각하는 두 분석의 차이에 대한 예시를 들어보고자 합니다.
“근육량과 운동시간은 어떤 관계 를 가질까?” – 상관분석
“근육량과 운동시간의 관계”를 밝혀내고 싶을 때, 상관분석을 하는 것이 맞습니다.
근육량, 운동시간이라는 두 변수의 상호 관계 또는 연관성을 볼 수 있기 때문에 상관분석을 통해 아래와 같은 결과를 볼 수 있을 것입니다.
1. 근육량과 운동시간은 무관하다.
2. 근육량과 운동시간은 양의 상관 관계를 가진다 (근육량, 운동시간 비례적인 관계).
3. 근육량과 운동시간은 음의 상관 관계를 가진다 (근육량, 운동시간 반비례적인 관계).
하지만, 상관분석으로 인과 관계를 밝힐 수 없습니다 . 애초의 두 변수에 대한 원인과 결과를 정의해두고 있지 않고, 연관성이나 상호 관계를 분석하는 방식입니다.
즉, 근육량과 운동시간이 양의 상관 관계를 가진다는 결과를 받았을 때, 근육량이 커서 운동시간이 긴 것일지 운동시간이 길어서 근육량이 큰 것인지는 정의하기는 어렵습니다.
상관분석에서는 변수 사이의 관계를 표현하고 수치를 보고자 하는 것입니다. 즉, 두 변수의 관계가 어떻고, 얼마나 강한 연결관계를 가지는 가를 수치, 척도로 표현합니다
<회귀분석>
“운동시간이 길기 때문에 , 근육량도 늘지않을까?” – 회귀분석
“근육량과 운동시간의 인과관계”를 밝혀내고자 할 때는, 회귀분석이 적합합니다.
운동시간이 길기 때문에 근육량에 주는 영향을 수학적인 모델 로 밝혀 낼 수 있을 것입니다.
회귀분석은 주어진 변수가 인과관계 를 가지고 었어야합니다.
하나 이상의 독립 변수(운동시간)의 변화가 종속 변수(근육량)의 변화를 추정하는 것이 목표입니다.
회귀분석은 독립 변수와 종속 변수의 관계를 수학적 모델로 밝혀낸다고 말씀드렸습니다.
그렇기 때문에 회귀분석을 통해 나오는 결과는 “어떠한 수학 식” 이 되고, 일반적인 회귀 분석법인 선형 회귀 분석은 아래와 같은 하나의 직선, 회귀선이라 불리는 수식을 찾는 과정입니다.
츌처 https://kkokkilkon.tistory.com/77
y= ax + b는 독립변수 x와 종속변수 y의 관계를 설명하는 수식이라 볼 수 있고, 이 수식을 통해 주어진 x 값을 통해 y값을 추정할 수 있습니다.
즉, 운동시간과 근육량이 위의 그래프와 같은 관계를 가진다면, 1시간 정도 할 경우 근육량이 어느 정도 늘어날 것인가를 추정해 볼 수 있을 것입니다.
결국 회귀분석 과정은 독립변수 x, 종속변수 y의 데이터가 산점도 그래프처럼 뿌려져 그려질 때, y=ax + b라는 최적의 회귀선을 찾아가는 과정을 말합니다.
최적의 회귀선? 두 변수 관계를 가장 잘 설명하는 회귀선!
가장 잘 설명하는 회귀선이라는 기준을 찾는 방법은?? 최소 제곱 법!
<최소 제곱 법>
최소 제곱 법을 설명하기 위해서는 잔차라는 개념을 먼저 알아야 합니다.
잔차란 관측값(실측값)의 y와 예측값의 y 간의 차이를 말합니다.
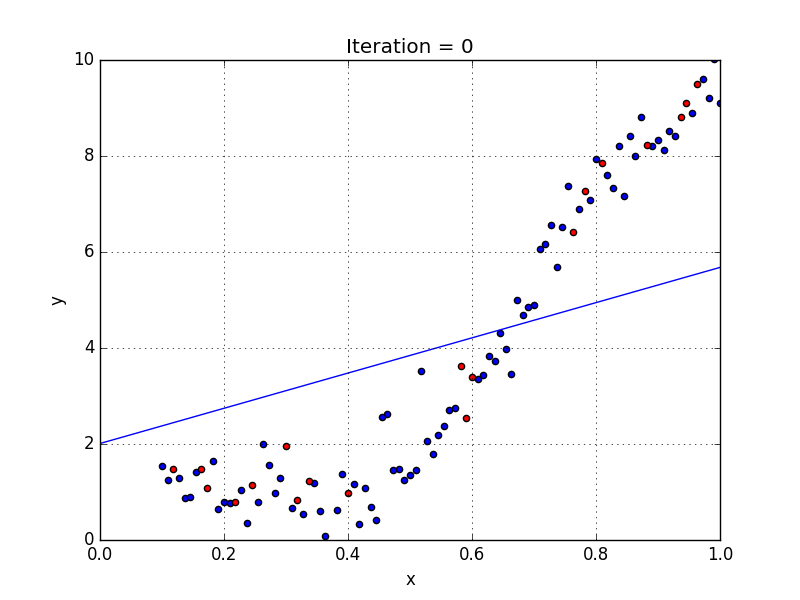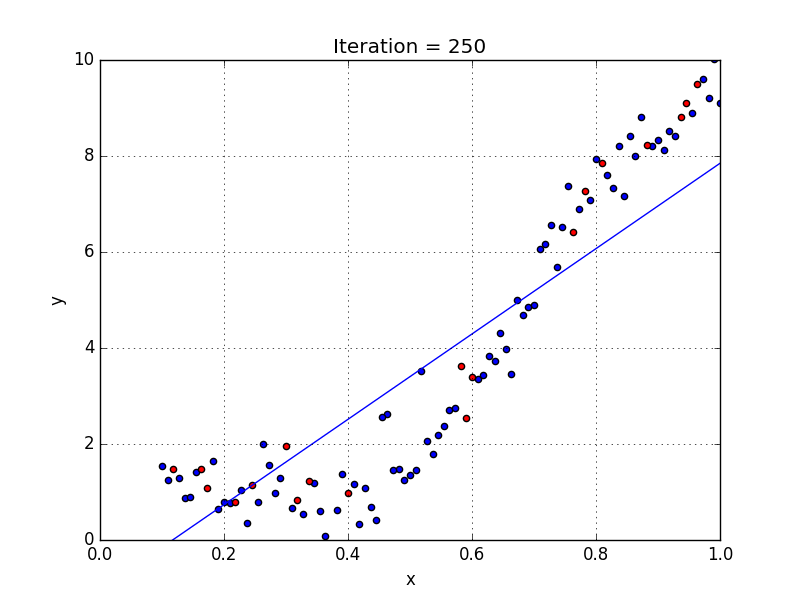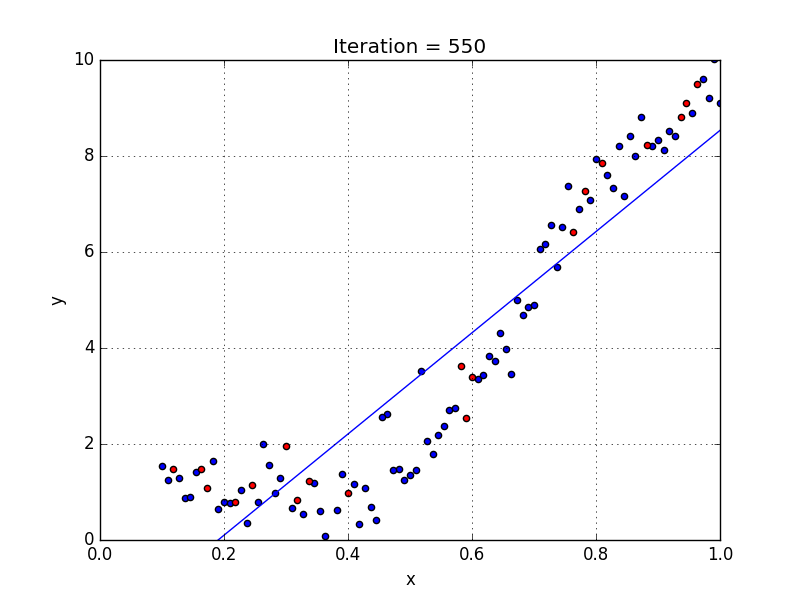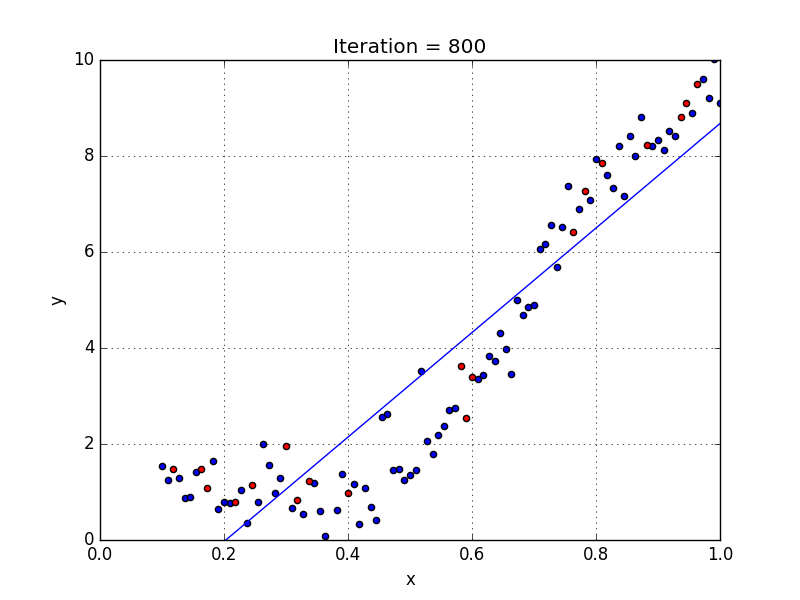
다시, 산점도 그래프로 뿌려진 데이터에서 가장 설명을 잘할 수 있는 회귀선 y = ax + b를 찾는 과정입니다.
이때, a와 b를 어떻게 갱신하느냐에 따라 회귀선이 달리 표현될 것입니다.
즉, a와 b에 의해 표현된 회귀선이 x, y의 관계를 가장 잘 설명해야하한다 라는 의미가 됩니다.
그래서 a와 b를 임의로 설정한 후 주어진 데이터 x를 넣어보면서 관측값(실측값) y와 차이가 없는지 계속 알아보면서 차이가 적은 그래프, 즉 가장 실측값에 가깝게 표현되는 회귀선을 찾아가는 방법입니다.
이 방법을 “최소 제곱 법”이라고 합니다.
예를 들어 A(1, 4)과 B(2, 3)라는 2개의 점이 있고 회귀 식이 f(x) = y = 2x + 1이라 합니다.
A의 관측값은 4이지만, 회귀선에 의해 예측된 값은 f(1)인 3입니다. 이때 A의 잔차는 1입니다.
B의 관측값은 3이지만, 회귀선에 의해 예측된 값은 f(1)인 5입니다. 이때 B의 잔차는 2입니다.
이때, 잔차의 제곱의 합은 5일 것입니다. 이 값이 가장 최소가 되는 회귀식을 찾아가는 것이 회귀분석의 과정입니다.
출처 https://wyn-associates.com/lr_pr/
<상관분석 vs 회귀분석 비교 차트>
출처 https://ko.gadget-info.com/difference-between-correlation
<내 생각>
상관분석은 결국 두 변수에 대한 관계성을 파악하고, 어느 정도 그 관계성이 강한가를 보는 것이고, 회귀분석은 인과관계에 있는 두 변수가 어떤 변화 양상을 가지는 지를 수학적 모델로 표현하고, 이 수학적 모델을 찾아가는 과정이라 이해가 되었습니다.
인공지능에서 하나하나의 노드(퍼셉트론)가 이러한 회귀분석을 통해 결과를 추출한다는 의미에 대해 더 명확하게 이해할 수 있었습니다.
인공지능의 레이어층들은 엄청난 회귀분석의 연속, 집합체라는 생각이 들었습니다.
<참고 자료>
https://ko.gadget-info.com/difference-between-correlation
https://kkokkilkon.tistory.com/77
728×90
상관 관계와 회귀의 차이
상관 관계 및 회귀 분석은 다 변수 분포를 기반으로 한 두 가지 분석입니다. 다 변수 분포는 여러 변수의 분포로 설명됩니다.는 ‘x’와 ‘y’의 두 변수 사이의 연관성 또는 연관성을 알 수있게 해주는 분석으로 설명됩니다. 반면에분석은 독립 변수의 알려진 값을 기반으로 종속 변수의 값을 예측합니다. 두 개 이상의 변수 간의 평균 수학적 관계를 가정합니다.
상관과 회귀의 차이는 인터뷰에서 자주 묻는 질문 중 하나입니다. 더욱이 많은 사람들이이 두 가지를 이해하는 데 애매 모호합니다. 따라서이 두 가지에 대해 명확하게 이해하려면이 기사를 자세히 읽으십시오.
비교 차트
비교의 근거 상관 관계 회귀 분석 의미 상관 관계는 두 변수의 상호 관계 또는 연관성을 결정하는 통계적 척도입니다. 회귀 분석은 독립 변수가 종속 변수와 어떻게 수치 적으로 관련되는지를 설명합니다. 용법 두 변수 간의 선형 관계를 나타냅니다. 최선의 라인을 맞추고 다른 변수에 기초하여 하나의 변수를 추정하십시오. 종속 변수 및 독립 변수 차이 없음 두 변수가 다릅니다. 나타냅니다 상관 계수는 두 변수가 함께 움직이는 정도를 나타냅니다. 회귀 분석은 알려진 변수 (x)의 단위 변경이 추정 변수 (y)에 미치는 영향을 나타냅니다. 목표 변수 사이의 관계를 표현하는 수치를 찾으려면. 고정 변수의 값에 기초하여 무작위 변수의 값을 추정합니다.
상관 관계 정의
상호라는 용어는 두 단어 ‘Co'(함께)와 두 개의 양 사이의 관계 (연결)의 두 단어의 조합입니다. 상관 관계는 두 변수를 연구 할 때 한 변수의 단위 변화가 다른 변수 즉, 직접 또는 간접 변수의 동등한 변화에 의해 보복 될 때 관찰됩니다. 그렇지 않으면 한 변수의 이동이 특정 변수의 다른 변수의 이동에 해당하지 않을 때 변수가 상호 연관성이 없다고합니다. 이것은 변수 쌍 사이의 연결 강도를 나타내는 통계 기술입니다.
상관 관계는 양수 또는 음수 일 수 있습니다. 두 변수가 같은 방향으로 움직일 때, 즉 하나의 변수가 증가하면 다른 변수가 증가하고 그 반대 인 경우 변수는 양의 상관 관계가있는 것으로 간주됩니다. 예를 들면 : 이익과 투자.
반대로 두 변수가 다른 방향으로 움직일 때 한 변수의 증가는 다른 변수의 감소를 가져오고 그 반대의 경우도 마찬가지입니다.이 상황을 음의 상관 관계라고합니다. 예 : 제품의 가격 및 수요.
상관 관계의 척도는 다음과 같습니다.
Karl Pearson의 제품 – 순간 상관 계수
스피어 만 순위 상관 계수
산포도
동시 편차 계수
회귀의 정의
둘 이상의 변수 간의 평균 수학적 관계를 기반으로 한 하나 이상의 독립 변수의 변화로 인한 메트릭 종속 변수의 변화를 추정하기위한 통계 기법을 회귀라고합니다. 그것은 과거 또는 현재의 사건을 기반으로 과거, 현재 또는 미래의 사건을 예측하는 데 사용되는 강력하고 유연한 도구이기 때문에 많은 인간 활동에서 중요한 역할을합니다. 예를 들면 : 과거 기록을 토대로 사업의 미래 이익을 예측할 수 있습니다.
간단한 선형 회귀 분석에서 x와 y의 두 변수가 있습니다. 여기서 y는 x에 의존하거나 x의 영향을받습니다. 여기서 y는 종속 변수 또는 기준 변수로 불리고 x는 독립 변수 또는 예측 변수입니다. x에 대한 y의 회귀선은 다음과 같이 표현됩니다.
y = a + bx
여기서, a = 상수,
b = 회귀 계수,
이 방정식에서 a와 b는 두 회귀 매개 변수입니다.
상관 관계와 회귀의 주요 차이점
아래에 주어진 포인트는 상관 관계와 회귀의 차이를 자세히 설명합니다.
두 양의 상호 관계 또는 연관성을 결정하는 통계적 척도를 상관 관계라고합니다. 회귀 분석은 독립 변수가 종속 변수와 어떻게 수치 적으로 관련되는지를 설명합니다. 상관 관계는 두 변수 간의 선형 관계를 나타 내기 위해 사용됩니다. 반대로 회귀 분석을 사용하여 최적의 변수를 구하고 변수 하나를 다른 변수를 기반으로 추정합니다. 상관 관계에서는 종속 변수와 독립 변수간에 차이가 없습니다. 즉 x와 y 간의 상관 관계는 y와 x와 유사합니다. 반대로, x에 대한 y의 회귀는 y에 대한 x와 다릅니다. 상관 관계는 변수 간의 연관성을 나타냅니다. 반대로 회귀 분석은 독립 변수의 단위 변화가 종속 변수에 미치는 영향을 반영합니다. 상관 관계는 변수 간의 관계를 나타내는 숫자 값을 찾는 것을 목표로합니다. 고정 변수의 값을 기준으로 임의의 변수의 값을 예측하는 회귀 분석과 달리
결론
위의 논의와 함께이 두 수학 개념은 큰 차이가 있지만, 이 두 이론은 함께 연구되었지만 분명합니다. 상호 관계는 연구자가 연구중인 변수가 상호 연관되어 있는지 여부를 알고 자 할 때 사용되며, 그렇다면 연관성의 강도는 무엇인가? 피어슨의 상관 계수는 상관 관계의 가장 좋은 척도로 간주됩니다. 회귀 분석에서 이벤트에 대한 미래 예측을하기 위해 두 변수 간의 함수 관계가 설정됩니다.
3. 회귀와 상관
3. 회귀와 상관 3.1. 단순회귀분석(單純回歸分析, simple regression analysis) 원인과 결과의 관계가 있는 두 변수를 분석-> 회귀분석
같은 개체에서 측정한 두개의 변수 -> Paired data 독립변수: 원인이 되는 변수
종속변수: 결과가 되는 변수 예) 한 개체의 일령과 체중과의 관계 일령: 다른 요인의 영향을 받지 않음 -> 독립변수 체중: 일령에 따라 다를 것으로 예상됨. -> 종속변수 예) 한 개체의 키와 체중과의 관계 -> 인과관계가 명확하지 않음 -> 상관 분석 종속변수와 독립변수 사이의 (선형)관계를 밝히는 방법
하나의 변수값을 알고 있을 때 이를 통해 다른 변수값을 예측하고자 하는 방법
별다른 설명 없이 ‘회귀분석’이라고 하면 일반적으로 ‘선형회귀분석’을 말함 이상값(outlier): 전체적인 추세에서 벗어난 값 이상값을 제거하거나, 제거하지 않음으로 회귀식의 추정 결과가 달라진다. 3.2. 회귀모형 적합도 회귀모형이 적합한지 확인하기 위해 결정계수 을 사용한다.
회귀모형의 독립변수가 종속변수 변동의 몇%를 설명하고 있는지를 나타내는 지표이다.
결정계수 가 1에 가까우면 -> 독립변수의 영향력이 크다.
즉 종속변수 변이의 대부분이 독립변수의 영향이다.
결정계수 가 0에 가까우면 -> 독립변수의 영향력이 작다. 출처: http://math7.tistory.com/123 예측값과 실제 값들 중 하나의 차이가 있을 때 오차 발생 예측값(직선)과 실제값과의 오차가 적은 것이 정확도가 높다. 점들이 선에 가까이 붙어 있다.
예측값(직선)과 실제값과의 오차가 큰 것이 정확도가 낮다. 점들이 선에 멀리 있다. 3.3. 다중회귀모형 어떤 변수에 영향을 끼치는 독립변수가 2개 이상인 경우 다중회귀라 한다. 3.3. 선형회귀와 비선형회귀 독립변수와 종속변수의 관계가 직선적이면 선형회귀라 하고, 곡선적이면 비선형회귀라 한다.
아래 그래프는 선형회귀로 볼 수도 있고, 비선형회귀로 볼 수 도 있다. 결국 값이 큰 것이 더 적합한 모형이라 본다. 3.3. 단순회귀의 이용분야 예측기능 : 년도별 우유소비량 추이 -> 미래의 우유소비량을 예측할 수 있다. 현재까지의 자료를 분석하여 미래를 예측한다. 먼 매래를 예측할수록 정확도가 떨어진다. 다른 변수에 의해 예측값이 크게 빗나갈 수 있다. 대체기능: 젖소의 BUN 측정치를 가지고 MUN 값을 추정한다. -> 간접측정 소의 흉위와 체중간의 관계에서 흉위를 측정하여 체중을 추정한다.
병아리의 정강이 길이를 측정하여 체중 발달 정도를 추정한다. 보정기능: 이유일령의 차이에 따른 이유시 체중을 보정
도살시 체중에 따른 등지방두께 보정 : http://gmgbreeding.com/new/sub02/sub02_03.php 실습: 다음 비육우 측정자료를 가지고 회귀분석을 실시한다. 흉위 체중 158 540 164 544 167 553 170 549 171 560 176 557 179 556 183 565 그래프 그리기: 주어진 자료로 분산형 그래프를 그리고 추세선츨 추가한다. 데이터 범위를 선택한다 ( A1:B9). 삽입 -> 분산형 그래프 계열 마커에서 마우스 오른버튼 -> 추세선 추가 선형, 수식을 차트에 표시, R-제곱 값을 차트에 표시 체크함. 최종 결과 3.4. 단순상관(單純相關, simple correlation) 두 변수간의 종속관계가 명확하지 않은 경우. -> 상관분석 상관계수의 범위: -1 ~0~1 0 -> 상관관계 없음. 양수 -> 정의 상관 또는 양의 상관(최대 1) 음수 -> 부의 상관 또는 음의 상관(최소 -1) 실습: 다음 4가지 자료를 가지고 상관분석을 실시한다(그래프 그리기). X Y 2 2 6 4 8 5 10 6 14 8 16 9 18 10 24 13 28 15 X Y 2 6 6 5 8 10 10 6 14 9 16 15 18 4 24 13 28 2 X Y 2 4 6 10 8 2 10 8 14 5 16 6 18 15 24 9 28 13 X Y 2 13 6 15 8 10 10 6 14 9 16 8 18 5 24 4 28 2 신체측정자료를 가지고 키 – 체중의 상관분석을 실시한다.
상관분석과 회귀분석 > 회귀분석
물론 그 모형은 모형적합도를 통하여 모형의 적합성을 확인될 것이다.
상관과 선형회귀분석의 차이는 그 목적성에 있다.
상관은 두 변수들간의 어떠한 관계 (relationship)의 세기를 측정하려는 것으로
유의성을 가설검정 (hypothesis test)를 위한 P-value로,
그 관계의 세기를 상관계수 r-value 또는 결정계수 r2로 표현한다.
선형회귀분석은 상관에서 더 나아가 인과관계의 정보까지 포함한다.
키워드에 대한 정보 상관 분석 회귀 분석
다음은 Bing에서 상관 분석 회귀 분석 주제에 대한 검색 결과입니다. 필요한 경우 더 읽을 수 있습니다.
이 기사는 인터넷의 다양한 출처에서 편집되었습니다. 이 기사가 유용했기를 바랍니다. 이 기사가 유용하다고 생각되면 공유하십시오. 매우 감사합니다!
사람들이 주제에 대해 자주 검색하는 키워드 상관분석 개념 설명- 깜신의 통계 왕초보 탈출 26탄
- 상관분석
- 통계인강
- 깜신
- 건양대학교병원
- 김종엽
- correlation test
- 상관분석은 회귀분석의 시작
상관분석 #개념 #설명- #깜신의 #통계 #왕초보 #탈출 #26탄
YouTube에서 상관 분석 회귀 분석 주제의 다른 동영상 보기
주제에 대한 기사를 시청해 주셔서 감사합니다 상관분석 개념 설명- 깜신의 통계 왕초보 탈출 26탄 | 상관 분석 회귀 분석, 이 기사가 유용하다고 생각되면 공유하십시오, 매우 감사합니다.