당신은 주제를 찾고 있습니까 “평균 변화율 공식 – 평균변화율과 순간변화율(미분계수)“? 다음 카테고리의 웹사이트 you.charoenmotorcycles.com 에서 귀하의 모든 질문에 답변해 드립니다: https://you.charoenmotorcycles.com/blog/. 바로 아래에서 답을 찾을 수 있습니다. 작성자 수악중독 이(가) 작성한 기사에는 조회수 67,861회 및 좋아요 1,042개 개의 좋아요가 있습니다.
평균 변화율 공식 주제에 대한 동영상 보기
여기에서 이 주제에 대한 비디오를 시청하십시오. 주의 깊게 살펴보고 읽고 있는 내용에 대한 피드백을 제공하세요!
d여기에서 평균변화율과 순간변화율(미분계수) – 평균 변화율 공식 주제에 대한 세부정보를 참조하세요
http://mathjk.tistory.com
평균 변화율 공식 주제에 대한 자세한 내용은 여기를 참조하세요.
[기본개념] 평균변화율 – 부형식 수학
이래서 평균변화율의 공식은 아래 두 가지를 암기하시면 됩니다. 쌤 두 가지나 암기해야 되나요? 어떻게 보느냐에 따라 긍정적으로 바뀔 수 있겠죠? 두 …
Source: bhsmath.tistory.com
Date Published: 1/8/2021
View: 9290
평균변화율 복습 (개념 이해하기) | 함수 – 칸아카데미
평균변화율을 복습하고 문제를 풀기위해 어떻게 적용하는지에 대해 알아봅시다.
Source: ko.khanacademy.org
Date Published: 1/17/2022
View: 8091
수학 개념 정리/공식 : 미분계수, 평균변화율, 미분계수의 …
Study Materials/고등 수학 개념 정리. 수학 개념 정리/공식 : 미분계수, 평균변화율, 미분계수의 기하학적 의미, 미분가능성과 연속성. 머니덕 2020.
Source: koreanfoodie.me
Date Published: 8/6/2021
View: 1624
변화량 – 나무위키:대문
미분에서는 이 기울기를 변화율이라고 부르게 되는데, 여기서 평균변화율은 두 점 사이의 그래프 전체의 기울기이다.
Source: namu.wiki
Date Published: 6/20/2021
View: 6651
평균 변화율 공식 by 한나 라 – Prezi
평균 변화율 공식 · Number of times this content has been viewed · Button to like this content · Button to share content · Button to report this content …
Source: prezi.com
Date Published: 11/14/2021
View: 6695
구간에서의 변화율에 대한 인식과 표현에 대한 연구
로 정의해서 순간변화율을 평균변화율의 극한으. 로 설명하고, 이 도함수의 함숫값을 함수. 의 해당 점에서의 접선의 기울기인 미분계수로. 도입한다.
Source: www.koreascience.or.kr
Date Published: 9/23/2022
View: 9874
주제와 관련된 이미지 평균 변화율 공식
주제와 관련된 더 많은 사진을 참조하십시오 평균변화율과 순간변화율(미분계수). 댓글에서 더 많은 관련 이미지를 보거나 필요한 경우 더 많은 관련 기사를 볼 수 있습니다.
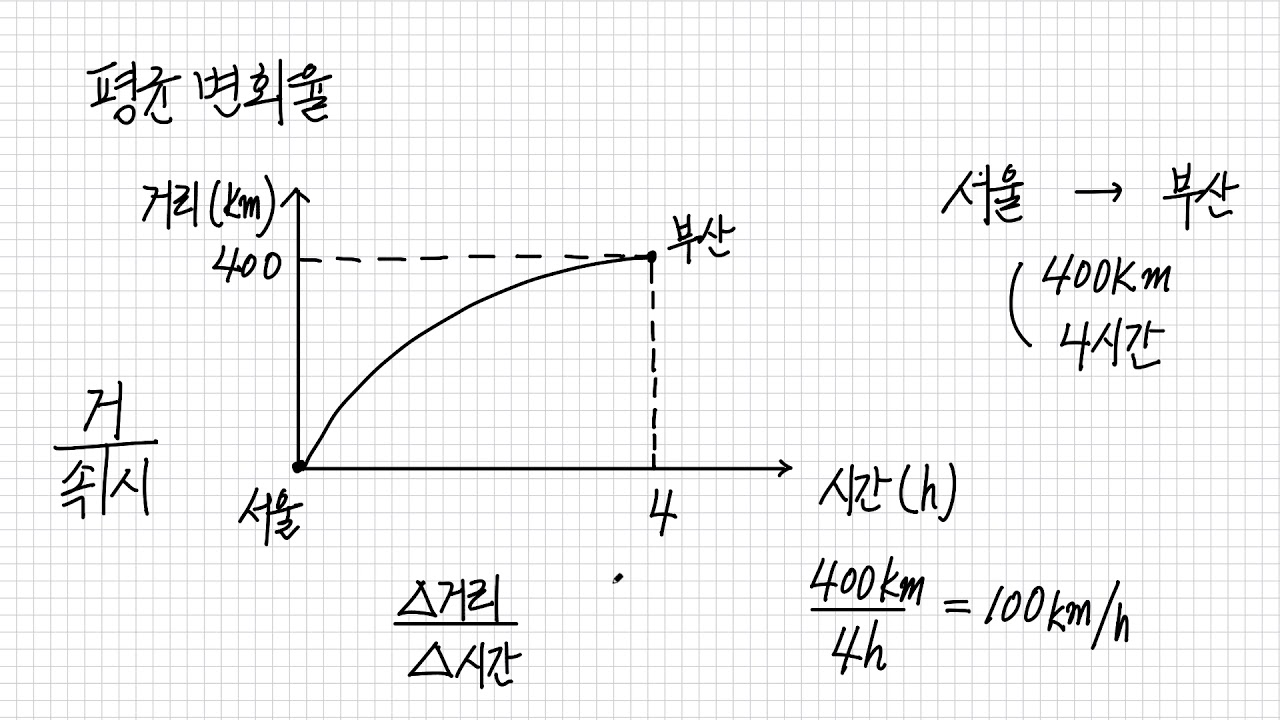
주제에 대한 기사 평가 평균 변화율 공식
- Author: 수악중독
- Views: 조회수 67,861회
- Likes: 좋아요 1,042개
- Date Published: 2018. 9. 19.
- Video Url link: https://www.youtube.com/watch?v=ixGZ0tg_lqs
수학 공식 | 고등학교 > 평균변화율과 미분계수
평균변화율
함수 $ y = f(x) $에서 $ x $의 값이 $ a $에서 $ b $까지 변할 때의 평균변화율은 \begin{gather*}
\frac{\Delta y}{\Delta x} = \frac{f(b) – f(a)}{b-a} = \frac{f(a+\Delta x) – f(a)}{\Delta x}
\end{gather*}
평균변화율의 기하학적 의미
평균변화율은 $ ( a, \ f(a) ) $, $ ( b, \ f(b) ) $를 잇는 직선의 기울기와 같다.
미분계수
함수 $ y = f(x) $의 $ x=a $에서의 미분계수는 \begin{gather*}
f'(a) = \lim_{h \rightarrow 0} \frac{f(a+h) – f(a)}{h} = \lim_{x \rightarrow a} \frac{f(x) – f(a)}{x-a}
\end{gather*}
미분계수의 기하학적 의미
미분계수 $ f'(a) $는 $ ( a, \ f(a) ) $에서의 접선의 기울기와 같다.
이차함수 $ f(x) = x^2 $에서 $ x $의 값이 $ 1 $에서 $ 3 $까지 변할 때의 평균변화율과 $ x=a $에서의 미분계수는 같다. 상수 $ k $의 값을 구하여라.
평균변화율은 \begin{gather*}
\frac{3^2 – 1^2}{3-1} = 4
\end{gather*} $ x=a $에서 미분계수는 \begin{gather*}
f'(a) = \lim_{h \to 0} \frac{(a+h)^2 – a^2}{h} = 2a
\end{gather*} 두 값이 같아야 하므로 \begin{gather*}
2a = 4 \ \ \ \therefore \ \ a=2
\end{gather*}
잡동사니
키워드에 대한 정보 평균 변화율 공식
다음은 Bing에서 평균 변화율 공식 주제에 대한 검색 결과입니다. 필요한 경우 더 읽을 수 있습니다.
이 기사는 인터넷의 다양한 출처에서 편집되었습니다. 이 기사가 유용했기를 바랍니다. 이 기사가 유용하다고 생각되면 공유하십시오. 매우 감사합니다!
사람들이 주제에 대해 자주 검색하는 키워드 평균변화율과 순간변화율(미분계수)
- 평균변화율
- 순간변화율
- 미분계수
평균변화율과 #순간변화율(미분계수)
YouTube에서 평균 변화율 공식 주제의 다른 동영상 보기
주제에 대한 기사를 시청해 주셔서 감사합니다 평균변화율과 순간변화율(미분계수) | 평균 변화율 공식, 이 기사가 유용하다고 생각되면 공유하십시오, 매우 감사합니다.

